What is Singularity?

Singularity

DEFINITION

The gravitational singularity or space-time singularity is defined as the location where the gravitational field of the celestial body is measured infinitely, which is not dependent on the coordinate system. These quantities are scalar invariant quantities of space-time curvatures, including the density of matter. The normal rules of spacetime cannot exist in a singularity.

What Is This Singularity?

Singularity, in short, is the absence of the Laws of Time and Physics.

So How Do We Explain?

First, let's talk about the first birth of the universe. If the universe came into being after a big bang (Big Bang), it will be questioned what happened before the explosion happened. This is where the concept of singularity comes into play. Here's how we explain it:

Before the big bang, there was a singularity, and a macro-level compression in the singularity exploded with such incredible power that it formed/is forming our universe. You might be confused here, "how about how?" I can hear you say. Let's put it this way, think about a person, and this person is getting old, the reason for his aging is time. Or it is gravity that makes us have weight, that is, physical laws in general. Now imagine that the two most important parts of this universe do not exist. Without Time and Physics, there is nothing. You can't argue that where there is no time and physics, something must happen, because it's literally nothing.

The Connection of Singularity and Black Holes

But the strange part here is that black holes form singularities. As you know, black holes are so powerful that they almost pierce the fabric of space-time. This means that when our universe, which is on a tissue, is punctured, a singularity occurs. This is, of course, according to the Big Bang theory. If we think according to the parallel universe theory, the singularity only existed when no universe was born. Because, according to the Parallel Universe Theory, black holes are transition holes to other universes. It actually sounds a bit utopian, but it makes sense in theory. The reason is that when black holes pierce the fabric of space-time, 1 pierces the structure of the universe, and what is outside of this space-time will be the space-time fabric of the other created universe. Based on this, each black hole will form a universe in the singularity within them. But for this he will have to exploit a universe. In short, the concept of singularity is more difficult to explain than the Parallel Universe Theory.

THE PENROSE SINGULATION AND BLACK HOLES

Penrose showed that, according to Einstein's general theory of relativity, there is a singularity at the center of all black holes, where gravity reaches infinity. Until Penrose's singularity theorem, physicists did not have a theory for how black holes form in nature.

Today we do not accept the existence of singularities, but we do agree that there is something like a singularity in black holes where the gravity is excessively increased. The Penrose singularity, however, helps explain not just black holes, but how the universe itself came into being with the big bang. After all, the big bang is also a kind of singularity. Let's see the origin of space-time and how it ends inside the black hole with the Penrose Singularity:

TIME IS FREEZING IN THE SINGLE PENROSE

Black holes have been a nightmare for our theories of gravity since the 1700s. When John Mitchell and Pierre Simon Laplace studied Newton's Law of Universal Gravity, they found that even light cannot escape from the surface of a star with a sufficiently large mass. Today, we know that the speed of escape from the surface of black holes is meaningless, because while black holes swallow light, they also absorb our future, forming a separate pocket universe within itself.

Mitchell and Laplace showed that theoretical celestial bodies with very strong gravity would catch even light and appear black in space. Today we know that light consists of photons, while photons are neither waves nor particles, but behave as particles or waves, depending on the situation. In short, we have learned that light is a very different phenomenon than predicted in classical physics.

Thus, black holes came to the fore for the first time after the 1700s: When Karl Schwarzschild solved the equations of general relativity, he showed that a ball of mass dense enough would create very strong gravity in a narrow space, and light, and therefore time, would freeze on the surface of the ball. Below the event horizon, which is the outer boundary of black holes, all matter, light and even space were destined to fall into a single central point inside the black holes. We call this the singularity in which the gravitational field strength reaches infinity.

HOWEVER, PHYSICISTS DO NOT LIKE SINGULATIONS

So why doesn't he like it? This is because singularities are infinitely small, infinitely dense points and creating an infinitely strong gravitational field shows the shortcomings in the theory of relativity. After all, when your theories start to give undefined expressions and infinities like 1/0, you think you've caught special cases where they don't work.

Einstein, too, did not believe that black holes could exist in the real universe. Even if there were black holes, there could be no singularity at the center. As a matter of fact, Schwarzschild's solution to the equation of relativity did not show how matter would clump together to form a singularity and event horizon. How could matter stack up and produce infinite gravity? It was impossible in classical physics to collect all matter in a single point.

Instead, Schwarzschild's solution showed that black holes, once formed, are stable and will exist forever (we know today that they will evaporate in the distant future with Hawking Radiation). Still, the idea of terrifying black holes that didn't let even light out continued to intrigue young physicists and encourage them to develop black hole physics.

PENROSES AND SUPERNOVAS

In 1939, Robert Oppenheimer and Hartland Snyder showed that a perfectly spherical and smooth dust ball would collapse as a theoretical Schwarzschild black hole, which does not revolve around itself and therefore does not exist in nature. In this ideal case, a singularity would have formed, which was very meaningful: If the dust grains were stacked on top of each other following a perfect collision course, they would all accumulate in the center and form a singularity, but this idea did not convince anyone. There was no perfect and smooth sphere in the universe!

Physicists did not think that chaotic atoms, particles, and particles in imperfect nature would be perfectly collected in one spot. Even the slightest deviation from spherical symmetry would cause the particles to miss each other at the last moment and disperse into space. For example, the substance that was collapsing in the center bounced back out again.

A massive star would deflate at the end of its life and collapse inward under its own weight, while rebounding and exploding outward. Today we know that some stars explode as supernovae, but their cores can collapse into black holes, or that stars can collapse directly into black holes, but we know all this thanks to Roger Penrose. How do you say:

PENROSE SINGULITY THEOREM

By the 1960s, Roy Kerr had found a real-life version of Oppenheimer and Snyder's solution to create a theoretical black hole. He deciphered the general theory of relativity and gave a physical description of rotating black holes. Since black holes are made up of stars and stars revolve around themselves, all black holes had to revolve around themselves. However, there was no point singularity at the center of Kerr black holes. Instead there was a 2D ring-shaped singularity.

However, since the Kerr solution is completely symmetrical, it did not show how black holes form in imperfect nature. Roger Penrose, then a young physicist at Cambridge, solved this problem. Mathematical physicist Penrose showed how black holes form in real life with his model of BLANK GEODESICS, which we will see shortly. Thus, he revealed that we can make progress in physics with pure mathematics, which shows that mathematics is not just a tool, but an inseparable part of physics. That's why the singularity theorem should be a buzzword for experimental physicists.

Only a few pages of paper Penrose published in 1965 seems trivial at first glance, but it shows mathematically how real physical systems can turn into black holes. So much so that the Penrose singularity is considered the most important development in relativity in the 50 years after the publication of the general theory of relativity. So how did this theory shed light on the singularity and deserve the Nobel Prize?

PENROSE AND BLANK GEODESICS

Penrose showed that regardless of the distribution of matter in space, when compressed in a small enough volume, an event horizon and a singularity would form. Imperfect clumping of matter did not prevent black holes. At least according to generality theory, and as for how: In relativity, mass bends space, and we represent it with a grid of twisted light rays. The shortest line between two points in curved space is a curve. So much so that the path followed by objects in free fall in a black hole-like gravitational field is called a geodetic (note that a satellite in space will also curve down to Earth).

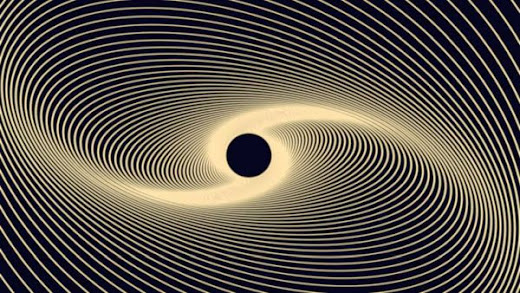
Whereas, in the singularity at the center of the black hole, space is bent so much that all curves, namely geodesics, intersect. In fact, as you can see in the picture, all geodesics intersect below and above the singularity! This shows why the light falling into the black hole cannot get out of the black hole even though it goes up.

Of course, you can say that the curves that light follows continue on their way after they intersect, but what we call a singularity in mathematics is a coordinate singularity. It is a point coordinate singularity, just like the intersection of longitude lines at the Earth's north and south poles. Yes, the singularity in a black hole is a physical singularity, but we know that there is no singularity in physics, it is a concept found in mathematics. On the other hand, we also know that Penrose showed black hole formation with a mathematical singularity.

This shows us how there is a relationship between mathematics and physics. Despite all these explanations, you can say that the lines diverge and continue on their way after they intersect, that is, there is no need for a singularity to form in the center of the black hole, but this is wrong.

PENROSE AND THE NORTH POLE

Just as an airplane goes north until it reaches the north pole, but continues on its way after reaching the pole, it lands south again; that is, just as there is no further north than the north pole, there is no space-time beyond the center of the black hole. The singularity bends space-time so much that matter and energy (light) focus on this mathematical point. Of course, the black hole does this by gravity, but remember that the speed of light is the speed of causation, and therefore of cause and effect:

When the Penrose singularity bends light, it bends space-time itself. Thus, it allows matter and energy to be collected in one spot, even though they are chaotic and imperfect. The bending of light by gravity is what we call a gravitational lens. So much so that the geodesics can continue on their way after intersecting in the singularity where space-time is bent at the degree of rupture; that is, negative energy and negative mass are the only ways that space-time can be reopened to form a black hole inverse white hole or wormhole:

You might call this the weak energy condition required for general relativity to describe phenomena in the universe. You can expand the negative energy singularity back into normal space-time, but you cannot dissipate the singularity because there is no negative energy and mass in the universe. Penrose thus reveals a mechanism that shows how natural black holes are formed in the theory of relativity: the intersection and rupture of geodesics.

EMPTY GEODESICS CROSS

If you ask what does the north and south poles of our Round Earth have to do with the inside of black holes, sir, according to Penrose's theorem, all points inside the event horizon, inside the black hole, are coordinate singularities that intersect like the polar longitudes on the world map. Of course, the entire black hole is not a singularity, but this geometric design shows how light falls into the central singularity. In summary, coordinate singularities show how a black hole bends space-time in such a way that light cannot escape.

PENROSE AND THE BIG EXPLOSION

Again, look at the drawing to understand why geodesics terminate when they intersect: The curves in the picture are the shortest lines between two points. However, if the curves continued after they intersect, we would have found lines shorter than the shortest line between two points. This is also a contradiction and indicates that geodesics should terminate as empty geodesics. This is what is meant by saying that the north pole has no north. That's why I described the event horizon, the outer boundary of the black hole, as a coordinate singularity, to show how the black hole inevitably absorbs light.

The event horizon is a kind of external singularity for us. It is the last limit in the universe where we cannot see the back of the horizon, that is, the inside of the black hole. The physical singularity inside the black hole is not the coordinate singularity. For us, light rays disappear into the event horizon as empty geodesics corresponding to the coordinate singularity (black holes… they are black and we cannot see inside).

In the central singularity, light rays disappear because space-time is bent to infinity. Geodesics are lost in point singularity in the non-rotating Schwarzschild black hole and in the ring-shaped singularity in the orbiting Kerr black hole.

As a result, Penrose's singularity theorem showed that we should take black holes seriously, but it didn't stop there: Black holes are singularities inside the real universe and will evaporate over time. However, the big bang that created the universe is also a point singularity in nothingness. So to understand the singularity of black holes is to understand how the universe came into being with the big bang. The black hole and the big bang singularity are not the same thing, but they can be explained with each other. Roger Penrose and Stephen Hawking did this 50 years ago:

PENROSE AND THE EXPANSION OF THE UNIVERSE

Physicists have known since the 1920s that the universe is expanding, and this was proven in 1964 when cosmic microwave background radiation was detected as the inevitable noise in radio telescopes. Hawking showed that when we rewind the universe to the big bang, space gets smaller and smaller, and light rays intersect and cut in the hot big bang as empty geodesics. He even pointed out that there is no point in time flowing before the big bang, considering that space-time is displaced inside black holes and time becomes space.

So much so that time turned into a three-dimensional surface like space and virtual time. Space and time were not created in the big bang, but before that they didn't make any sense. At the time of the big bang, space was a one-dimensional phenomenon and would have disappeared in the singularity. Time, on the other hand, was a surface on which time actually did not flow. Just like the event horizon, which is the outer boundary of a black hole...

Now attention: we know that due to the uncertainty principle in quantum physics, matter and energy will not be perfectly concentrated in one spot, despite empty geodesics. So there are no physical singularities in the real world, but what difference does it make?

For a black hole to create a gravitational field that doesn't let light out, it doesn't have to have a dimensionless, infinitely gravitational singularity at its center. Instead, a half-singularity, singularity-like, where gravity approaches infinity but is finite, is sufficient. The big bang could be such a half-singularity.

VIRTUAL SINGULITY

We did not develop a quantum theory of gravity by combining general relativity with quantum physics, but quantum physics shows us that true singularities cannot occur. The fact that the singularity gives infinities in the general relativity equations also shows that relativity does not actually work on a microscopic scale. Despite this, Hawking found an equation that unified the geometry of relativity with quantum physics. This was not a quantum theory of gravity, but a kind of block time model that showed that the big bang could be a half-singularity:

LINE INTEGRALS

Before Hawking passed away in 2018, he was working on the line integrals conjecture. Accordingly, the big bang is the rounded 4D surface of the 5D hypersphere (roughly similar to the latitude-longitude lines of the earth in schools) consisting of 3-dimensional virtual time and one-dimensional virtual space. Stephen Hawking said that the universe is not infinite and you can read this model in the mirror universes articles. The part of line integrals that interests us is this:

If there is no true singularity at the time of the big bang, there are no empty geodesics. Space-time is infinitely rigid, and rays of light (curved geodetic lines) come close to each other almost to intersect, but not completely. So there could be another universe that shrank and disappeared before our universe, but exists forever, like a ghost in virtual space-time. Depending on how you solve the line integral equations, our universe may have been formed by the collapse of a predecessor universe as a black hole and then re-expansion, as Lee Smolin said. We call this the big tab theory.

THE ENDLESS UNIVERSE RANGE

The universe may be the last link in the endless cycle of universes formed by the contraction-big rebound-contraction cycle, or it may also be derived from a non-collapsed universe according to Penrose's harmonious cyclical cosmology theory. When the previous universe expands forever and the matter and energy it contains become extremely diluted, space-time turns into virtual space-time, and a new big bang may be triggered.

Nor does it have to be a universe that precedes our universe. It could also be the mirror universe mate of our universe. So much so that the two universes originate from the same big bang as in the picture, and time flows into the future in both, and both universes expand in opposite directions. Hawking's big bang theory based on line integrals that create virtual time is too long to cover here, but at least it shows why Penrose's singularity theorem deserves the 2020 Nobel Prize in Physics.

Penrose allowed us to investigate how the universe came into being with the big bang through black holes. Thus, he shared the Nobel Prize with Andrea Ghez and Reinhard Genzel, who tracked the trajectories of superfast stars at the center of the Milky Way and showed that they actually revolved around the supermassive black hole Sagittarius A*. This is how his article published in 1965 revolutionized physics.

FINAL SAY

Virtual space-time is real space, that is, how centered and correct is the setting of the environment to mean space in order to maintain its virtual title accordingly. It is debatable how healthy it is to call virtual space to the "environment" where there are virtual variables that spread quantum virtual existence and extinction. In our universe, Hawking Radiation and transmission at quantum wavelengths in space-time also see the boundaries of existence and disappearance, which is useful for evaluation. If we see it in our universe, can't this really be in the pre-universe? In other words, doesn't it mean that the things we call nothingness, which arise from being just the means they protect, already have their own burden and exist on this "nature" in the environment? Doesn't the existence of nature pose another problem for this "nature"? Why didn't this nothingness continue on its own and the universe came into being? Because the emergence of the exit of the house is actually contrary to what this nothingness carries. Because nothingness formulates its own nature in detail and reveals existence like atomic matter, our planetary galaxy and us. In such a picture, wouldn't it be a very strange situation for nothing to reveal this universe and what we see? In other words, the universe has been formed according to the rules of the nothing we see in the universe. It seems that the rules of nothingness and the universe it carries have formulated the physical structures and energy-matter structure that we see today and revealed the universe. In this case, the fundamental physics of the universe would not carry quantum physics, so we see quantum physics in the deepest bed of the house. As a result, wouldn't the thing called virtual space-time be the reflection of the universe formulas of nothingness to us? Also, doesn't this mean that it doesn't make a difference in essence between nothingness and our universe? Because basically nothingness gives rise to our universe, and since the essence of universes nevertheless derives from this nothingness and still continues to encounter the hosting and event of nothingness, wouldn't it actually be nothingness? If this is true, then why do we exist and why live a life where this nothingness is reflected as being?

We have come to the end of our article, and I would like to thank my teacher for his resources. Hope to see you again in a new article...

Kaynaklar:Wikipedia